部品実験:受動素子

元に戻る

事前知識　2024/6/30

本文目次		本文以外目次
１．R、C、Lの関係式 ２．直流のRC回路 ３．交流のRC回路（ローパスフィルター） ４．直流のRL回路 ５．交流のRL回路（ハイパスフィルター）

本　　　文

受動素子とは電気エネルギーの増幅や整流をしない部品ということで、抵抗・コンデンサ・コイルを言います。 ここではこの受動素子が電気的にどのような変化をさせるのか、シミュレーションや実際に実験をしてみたい。 １．R、C、Lの関係式 R、C、Lの関係式をふりかえってみる。 部品 抵抗 コンデンサ コイル リアクタンス 電圧式 電流式 電流位相 電圧と同じ 電流が進み 電流が遅れ [目次に戻る]

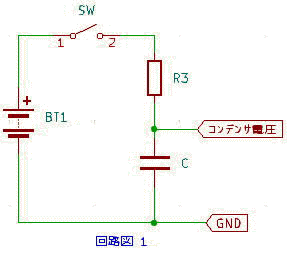
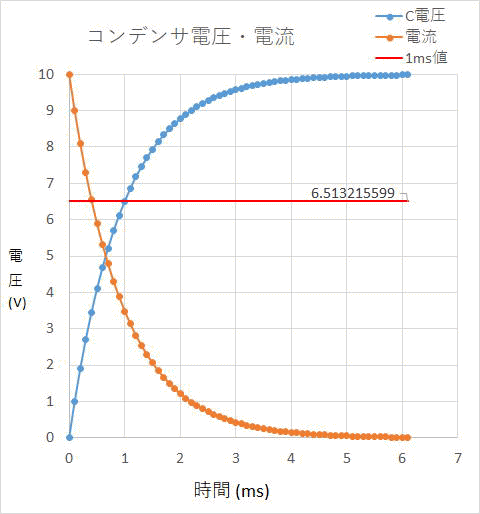
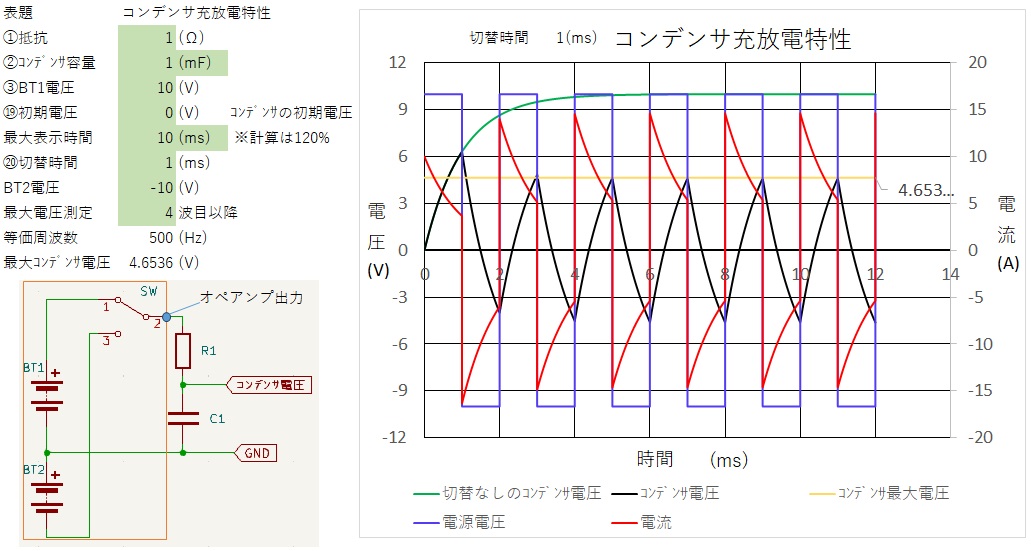
２．直流のRC回路 　直流電源に抵抗とコンデンサを組み合わせた回路の電圧と電流の変化について 考えて見る回路としては左図のような回路を想定する。 SWを入れた後、どのようにコンデンサ電圧や回路の電流が変化するかを考えてみる。 仮定として BT1＝10(V) R3＝１(Ω) C＝1(mF) とする。 簡単に計算して様子を確認するため、微分とかは使用せず、ある時間間隔で計算するものとする。 ある程度の傾向が判れば良いと思うので、ある程度の誤差が出来る事は承知ください。 時間間隔は0.1(ms)間隔とする。 ■簡易計算手順は下記のとおり。-- ① スイッチを入れた直前にはCのコンデンサには電荷（＝0＝0(V)）がないため、電流は 　(BT2電圧-C電圧)/R3＝10/1＝10(A) 　となります。 ②Cへ蓄積された電圧 　・V(V) = Q(C)/C(F) 　・Q(C) = I(A)×T(s) 　以上から　V(V) = I(A)×T(s)/C(F) となることから 10(A)の電流が0.1(ms)間Cに流れた場合のCの電圧は 　10×0.1×10-3／1×10-3＝1(V) 　となります。 ③Cの電圧は 　スイッチを入れた時にCのコンデンサに電荷が無かったので、0.1ms後の電圧は 　前のCの電圧+②の電圧＝1(V) ④スイッチをいれてから0.1(ms)後のコンデンサの電圧②と電流①から 　(10-1)／1＝9(A) ②へ戻って計算を繰り返す。 　と言うことで　①～④を繰り返し計算(EXCELワークシート)した結果を下表に示します。 コンデンサ充電イメージ 経過時間 (ms) C電圧 (V) BT2-C電圧 (V) 電流 (A) Cの 増加電圧 (V) 0 0 10 10 1 0.1 1 9 9 0.9 0.2 1.9 8.1 8.1 0.81 0.3 2.71 7.29 7.29 0.729 0.4 3.439 6.561 6.561 0.6561 0.5 4.0951 5.9049 5.9049 0.59049 0.6 4.68559 5.31441 5.31441 0.531441 0.7 5.217031 4.782969 4.782969 0.4782969 0.8 5.6953279 4.3046721 4.3046721 0.43046721 0.9 6.12579511 3.87420489 3.87420489 0.387420489 1 6.513215599 3.486784401 3.486784401 0.34867844 1.1 6.861894039 3.138105961 3.138105961 0.313810596 --　グラフ　１　-- 電圧の上昇は正比例で変化していないことが判ります。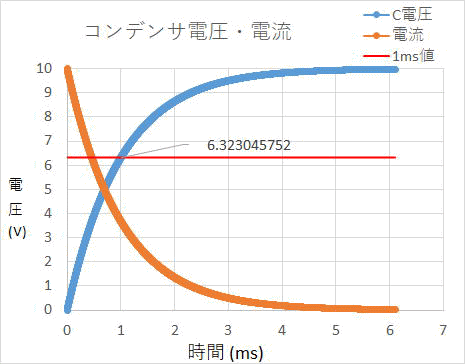 なお誤差があると言うことについては、 計算する時間間隔について0.01(ms)と0.001(ms)で計算した1(ms)後のコンデンサ電圧を計算した結果は 0.01(ms)間隔で計算　コンデンサ電圧　6.3396・・(V) 経過時間 ms C電圧(V) BT2-C電圧(V) 電流(A) Cの増加電圧(V) 1 6.339676587 3.660323413 3.660323413 0.036603234 0.001(ms)間隔で計算　コンデンサ電圧　6.3230・・(V) 経過時間 ms C電圧(V) BT2-C電圧(V) 電流(A) Cの増加電圧(V) 1 6.323045752 3.676954248 3.676954248 0.003676954 計算する時間間隔を小さくすることによコンデンサ電圧が小さくなっている。 だいぶ脱線しましたが、C電圧を計算する公式は になります。　e=ネイピア数 上記式で1(ms)後の電圧を求めると　6.3212･･(V)になります。 詳細は 【RC直列回路の微分方程式】『過渡現象』の解き方！ をご参照ください。 --　グラフ ２　-- ［0.001(ms)間隔で計算した場合のグラフ］ 以上から上記簡易計算方法では正確な値にはならないことが判りますが、計算する時間間隔を小さくすることにより、コンデンサ電圧の差が小さくなっている（誤差が少なくなっている）ことから、微積分や公式が判らなくても、許容出来る誤差の範囲で、計算する間隔を小さくする事によりシミュレーションとして使用出来ることが判ります。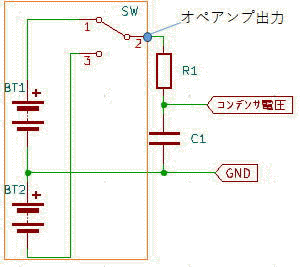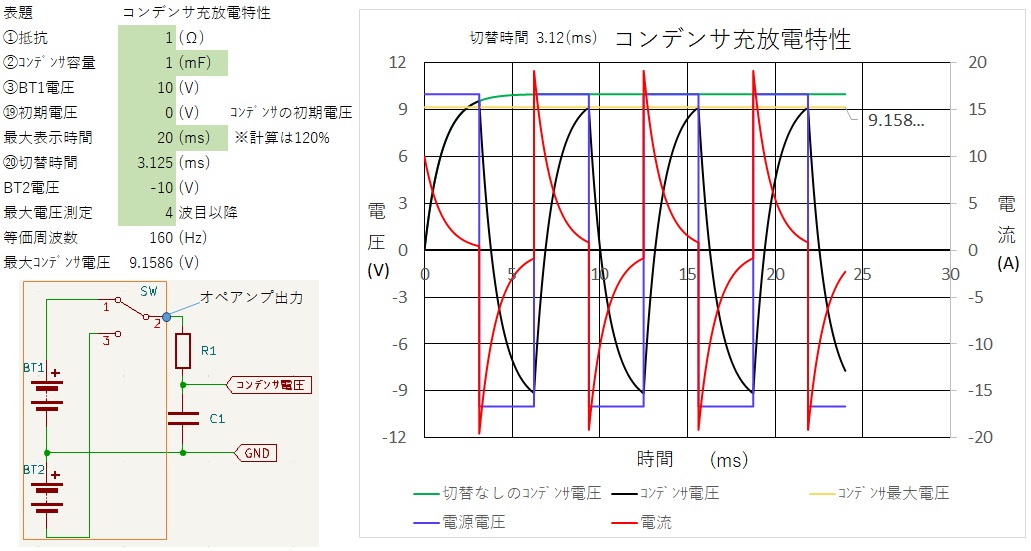 計算間隔 ①(ms) 各計算電圧 ②(V) ②と公式差 (V) 0.100 6.5132 0.192 0.010 6.3347 0.013 0.001 6.3230 0.002 公式 6.3212 基準 また上記のグラフでCRの値から上昇する具合が違うため、それを表すため時定数と言うものがあります。 この値は C(F)×R(Ω)で求めます。 この時のコンデンサ電圧は≒0.63212E　になります。(1-1/e)E 　上記計算時間間隔を変化させた時の1(ms)後のコンデンサ電圧を参照ください。 　許容できる誤差では使用できるかもしれません。 非常に脱線しましたが、上記RC回路は一般的に多くの回路にあり、信号に遅れ時間が重要なものについては、検討が必要になります。 例えば、下記回路の〇部分はU1Aのオペアンプ信号でQ1ゲートを制御してQ1のドレイン－ソース間をスイッチすること回路ですが、ゲート制御については8(V)以上でQ1のドレインーソース間がONになるとした場合を間考えて見ます。 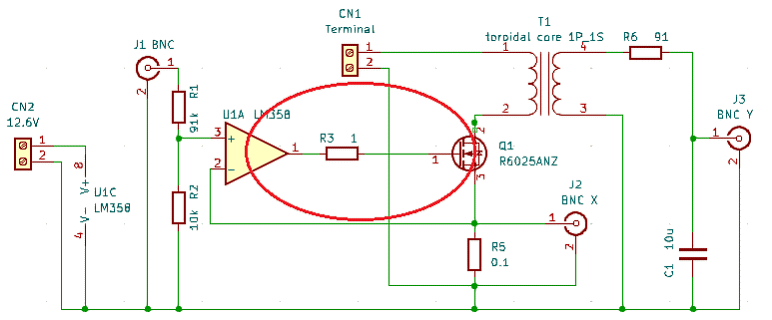〇の回路は下記の回路図になります。 条件 　R3＝R１＝１(Ω)　C１＝1(mF)　BT1＝10(V)　BT2＝-10(V) 　　　C1はQ1の入力容量Ciss　を示す。 　コンデンサ電圧が8(V)以上になればQ1のドレインーソース間がONになるのですが、先のグラフ２を見ても判りますが、SWの切替時間が1(ms)以下では8(V)にならないため、Q1が動作しないことが判ると思います。 　SWを1(ms)で切り替えた場合のシミュレーション結果を下記グラフに示す。 　なお下記ｺﾝﾃﾞﾝｻ最大電圧は安定後の最大電圧を見るため、左最大波を１波として何波目（設定は４波目）の最大電圧値を示している。 　直流の場合の電源変化ではBT2は0(V)ですが、後の交流波形と比較しやすいように今回はBT2＝-10(V)にしている。 一般的な回路で例えると、　ＦＥＴのゲート回路にもあり、これが動作周波数の上限にも関係している。 この概要は部品実験トランジスタのFETの予備知識で説明します。 またQ1を確実に動作させたい場合のSW切替時間を3.125(ms)[160Hz相当]にした場合の電圧状態を下記グラフに示す。 オペアンプから出力されている波形は10(V)又は-10(V)の矩形波です。 SW切替時間からこの矩形波の周波数は切替時間が1(ms)の場合1周期が1(ms)×2になるため周波数＝1000/(1×2)≒500(Hz) この時の最大電圧は≒4.65(V)、3.125(ms)では1000/6.25≒160(Hz)で最大電圧は≒9.16(V)となります。 ここで違った見方をしますが、電源周波数が高い場合はコンデンサ電圧が低く、電源周波数が低い場合はコンデンサ電圧が高くなっています。 このことから、この回路を低い周波数成分ほど良く通す（ローパス）フィルターとして使用出来る事が判ると思います。 しかし今回は信号が矩形波だったので、ローパスフィルターを使用するのは波形が正弦波の信号（交流）なので、正弦波の場合のコンデンサ電圧を次に確認したいと思います。 [目次に戻る]

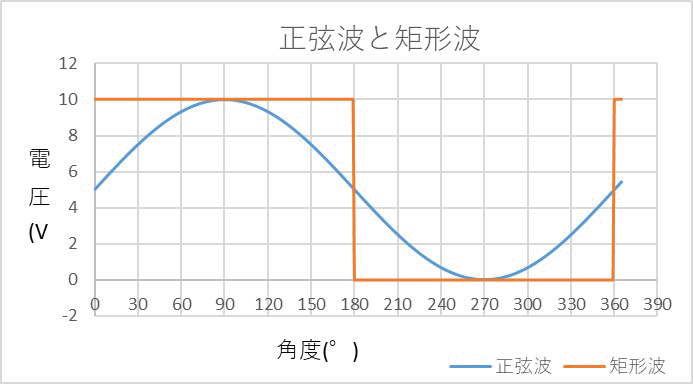
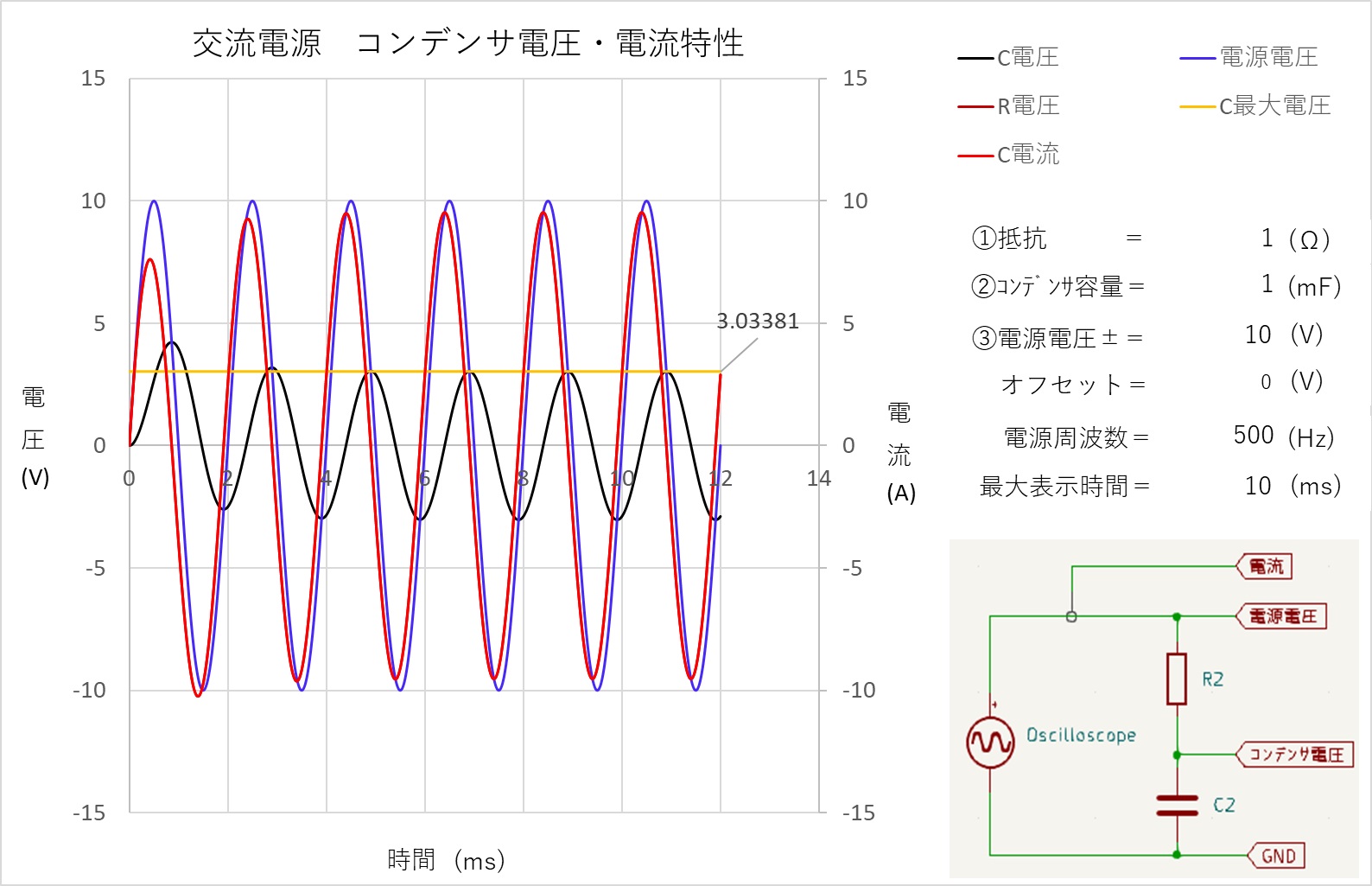
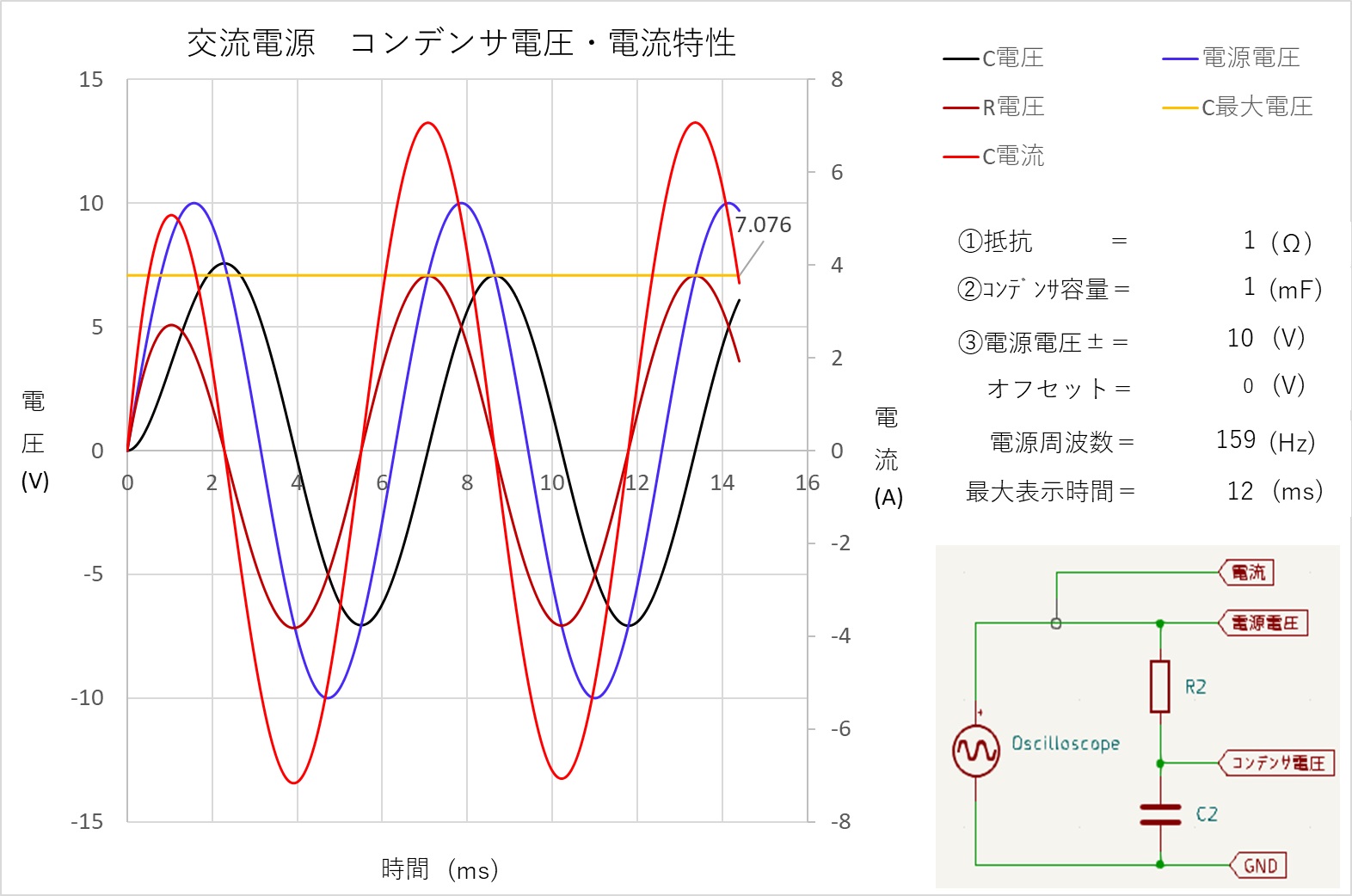
３．交流のRC回路（ローパスフィルター） 交流電源に抵抗とコンデンサを組み合わせた回路の電圧と電流の変化について。 電源波形が矩形波と正弦波ではコンデンサに流れる電流はどうなるのでしょうか。 右に正弦波と矩形波を描いたグラフですが、簡易計算で電流を求める計算方法で違いを見ると。 最初の電源電圧が矩形波では10(V)ですが正弦波では5(V)になるため、ここで電流が10(A)と5(A)と違いが出てくるため、コンデンサの電圧が違う事が判ります。 電流波形やコンデンサの電圧波形を頭の中で想像してみてください。 簡易計算で求めた波形を下記にしめします。 ■電源周波数500(Hz) 矩形波の時は4.65(V)に対し 正弦波の最大電圧は 　3.03381(V) になっている。 ■電源周波数159(Hz) 矩形波の時は9.16(V)に対し 正弦波の最大電圧は 7.076(V) になっている。 なおローパスフィルター関係には下記公式がある。 ゲイン　 　出力電圧 / 入力電圧　＝増幅率を言う　上記簡略式で言う　電源電圧 / ｺﾝﾃﾞﾝｻ電圧 となる。 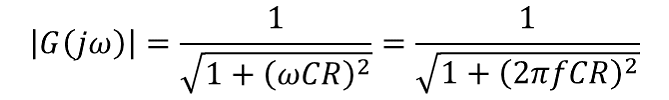　増幅率を電力dbで表示する場合は下記式になる。 位相差 　入力電圧と出力電圧の位相差を言います カットオフ周波数 　電力値が半分になる周波数を言います。　db表記で-3dbです。 　従って電圧で表記する場合は1/√2 ≒ 0.7071 となる。 上記公式から作成出来るグラフを下記に示す。 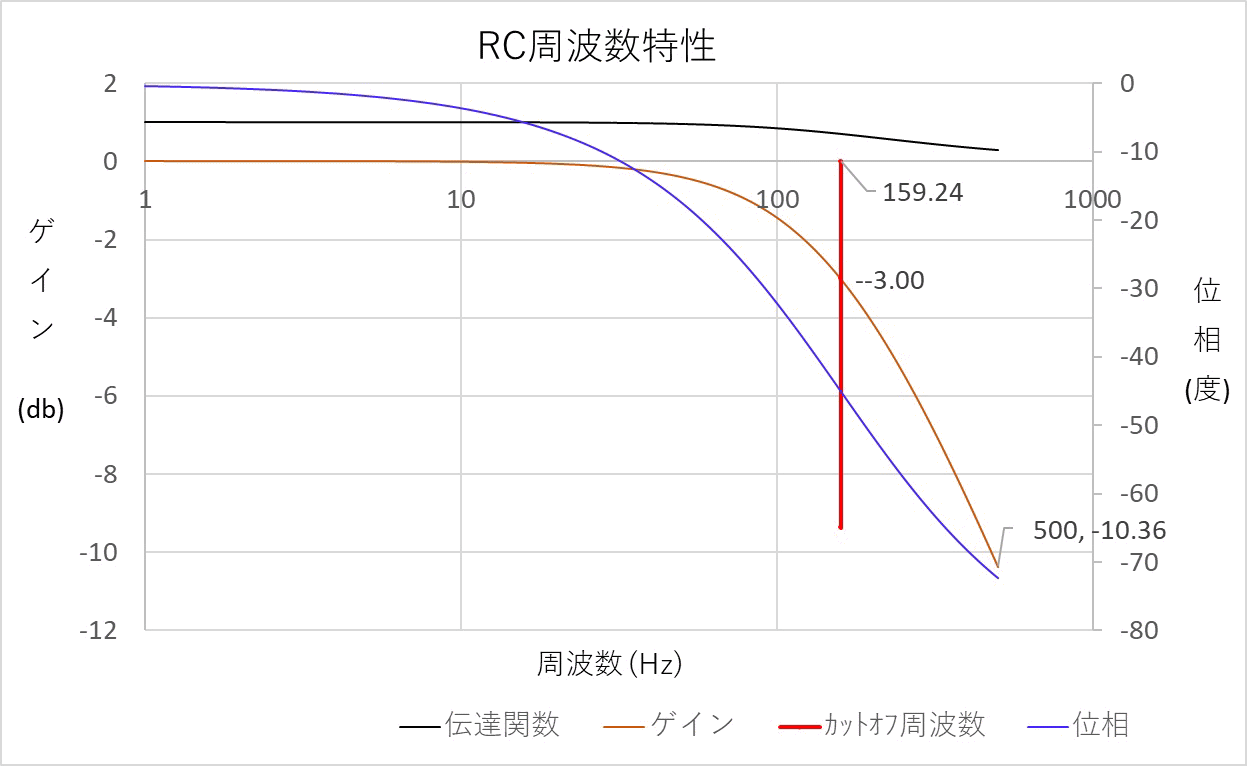ちなみに 　159Hz ゲイン　-3.0039db 　電圧は0.70763×10(V) 　≒　 7.076(V)　位相差は45° 　500Hz ゲイン　-10.36db　 　電圧は0.3034×10(V)　　≒　 3.034(V) でした。 次はRL回路を見てみたいと思う。 [目次に戻る]

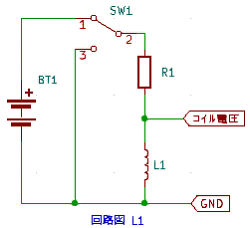
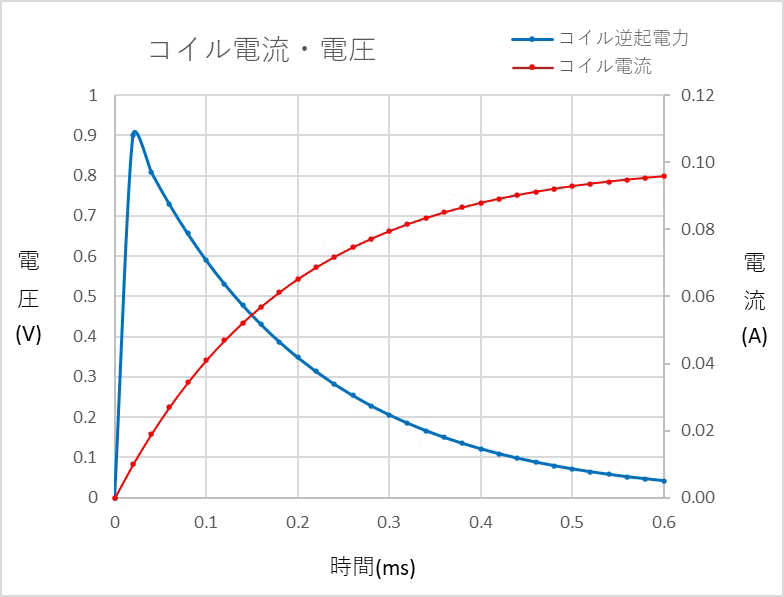
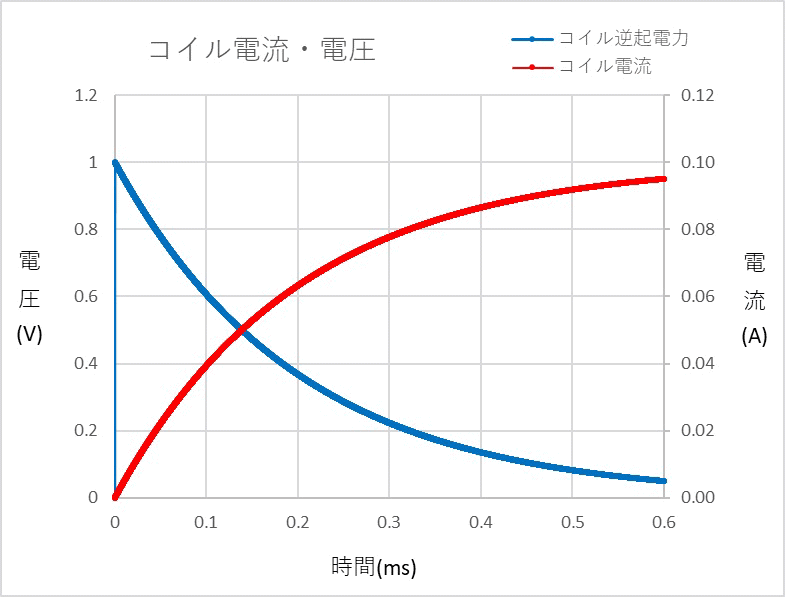
４．直流のRL回路 (1)直流電源に抵抗とコンデンサを組み合わせた回路の電圧と電流の変化について 考えて見る回路としては左図のような回路を想定する。 SWを入れた後、どのようにコンデンサ電圧や回路の電流が変化するかを考えてみる。 仮定として BT1＝1(V) R3＝１0(Ω) L1＝2(mH) とする。 簡単に計算して様子を確認するため、微分とかは使用せず、ある時間間隔で計算するものとする。 ある程度の傾向が判れば良いと思うので、ある程度の誤差が出来る事は承知ください。 時間間隔は0.02(ms)間隔とする。 ■簡易計算手順は下記のとおり。-- ●経過時間０ ①累積電流＝０ ②コイルの起電力＝０ ③必要コイル逆起電力 　＝電源を入れた時の電源電圧－抵抗電圧降下分（０） ④必要電流増加分 　＝③必要起電力（V）×Δ時間（s） / 自己ｲﾝﾀﾞｸﾀﾝｽ(H) ●次の時間 ①累積電流 　＝先の電流累積＋先の必要電流増加分 ②コイルの逆起電力 　＝電源電圧－抵抗電圧降下分（抵抗値×①） ③必要コイル逆起電力 　＝電源電圧－抵抗電圧降下分（抵抗値×先の①） ④必要電流増加分 　＝③必要起電力（V）×Δ時間（s） / 自己ｲﾝﾀﾞｸﾀﾝｽ(H) 　と言うことで　①～④を繰り返し計算した結果を下表に示します。 経過時間 (ms) ①IL （A) ②V (V) ③V’ (V) ④ΔIL (A) 0 0.0 0 1 0.01000000 0.02 0.010000 0.9 0.9 0.00900000 0.04 0.019000 0.81 0.81 0.00810000 0.06 0.027100 0.729 0.729 0.00729000 0.08 0.034390 0.6561 0.6561 0.00656100 0.1 0.040951 0.59049 0.59049 0.00590490 0.12 0.046856 0.531441 0.531441 0.00531441 0.14 0.052170 0.478297 0.478297 0.00478297 0.16 0.056953 0.430467 0.430467 0.00430467 0.18 0.061258 0.387420 0.387420 0.00387420 0.2 0.065132 0.348678 0.348678 0.00348678 0.22 0.068619 0.313811 0.313811 0.00313811 --　グラフ　１　-- 電圧の上昇は正比例で変化していないことが判ります。 なお誤差があると言うことについては、 計算する時間間隔について2(us)と0.2(us)で計算した2(ms)後のコイル電流を計算した結果は 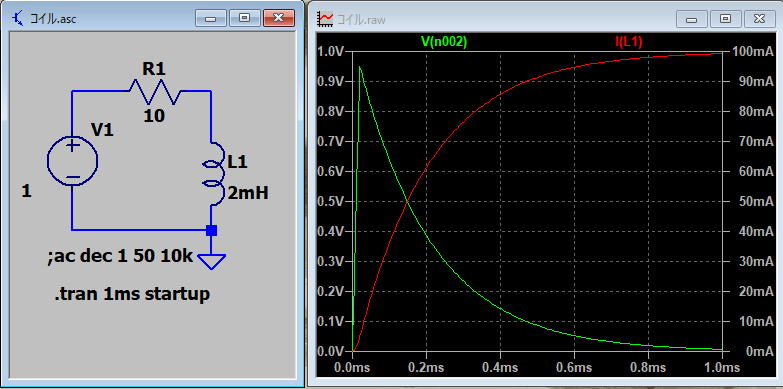2(us)間隔で計算　コイル電流　0.063231・・(A) 経過時間 (ms) ①IL （A) ②V (V) ③V (V) ④ΔIL (A) 0.2 0.063231 0.376934 0.376934 0.00003677 0.2(us)間隔で計算　コイル電流　0.063214・・(A) 経過時間 (ms) ①IL （A) ②V (V) ③V' (V) ④ΔIL (A) 0.2 0.063214 0.367861 0.367861 0.00000367 計算する時間間隔を小さくすることによコンデンサ電圧が小さくなっている。 だいぶ脱線しましたが、C電圧を計算する公式は になります。　e=ネイピア数 上記式で0.2(ms)後の電流を求めると　･･(A)になります。 詳細は 【RL回路の時定数】求め方や単位などを詳しく解説！ をご参照ください。 --　グラフ ２　-- ［0.2(us)間隔で計算した場合のグラフ］ 以上から上記簡易計算方法では正確な値にはならないことが判りますが、計算する時間間隔を小さくすることにより、コイル電流の差が小さくなっている（誤差が少なくなっている）ことから、微積分や公式が判らなくても、許容出来る誤差の範囲で、計算する間隔を小さくする事によりシミュレーションとして使用出来ることが判ります。 計算間隔 ①(ms) 各計算電流 ②(A) ②と公式の 差電流(A) 0.02 0.065132 0.001920 0.002 0.063231 0.000019 0.0002 0.063214 0.000002 公式 0.063212 　基準 今まではEXCELでシミュレーションしてきましたが、LTspiceと言うシミュレーションソフトで先の特性を表示すると の様に表示されます。 今後LTspiceを使用してシミュレーションしようと思います。 なおLTspiceについては当ページでは　LTspice[ここをクリック]　で紹介しています。 (2)時定数 　上記のグラフでLRの値から時間当たりの変化が違うため、それを表すため時定数と言うものがあります。 この値は L(H)/R(Ω)で求めます。　上記値からは0.2(ms)と言う答えになると思います。 　この時のコイル電流は≒0.063212(A)　になります。 　上記計算時間間隔を変化させた時の0.2(ms)後のコイル電流を参照ください。 　許容できる誤差では使用できるかもしれません。 非常に脱線しましたが、上記RL回路は一般的に多くの回路にあり、信号に遅れ時間が重要なものについては、検討が必要になります。 [目次に戻る]

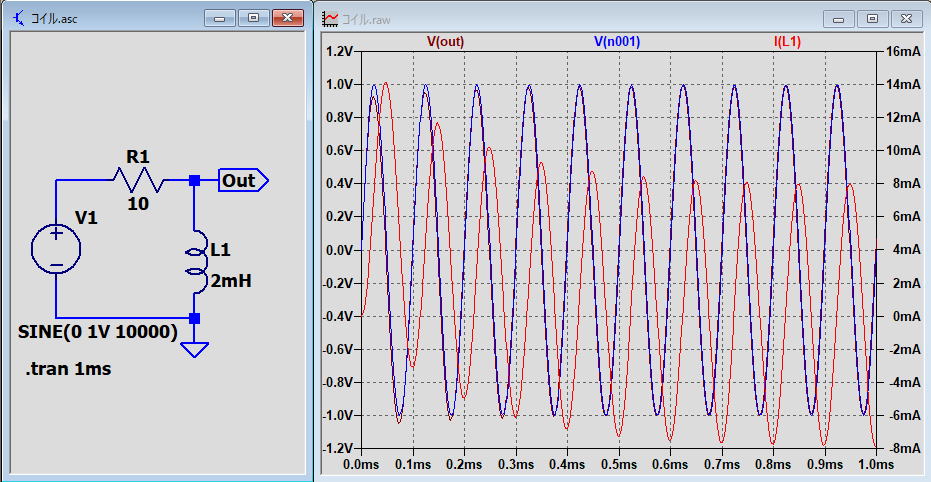
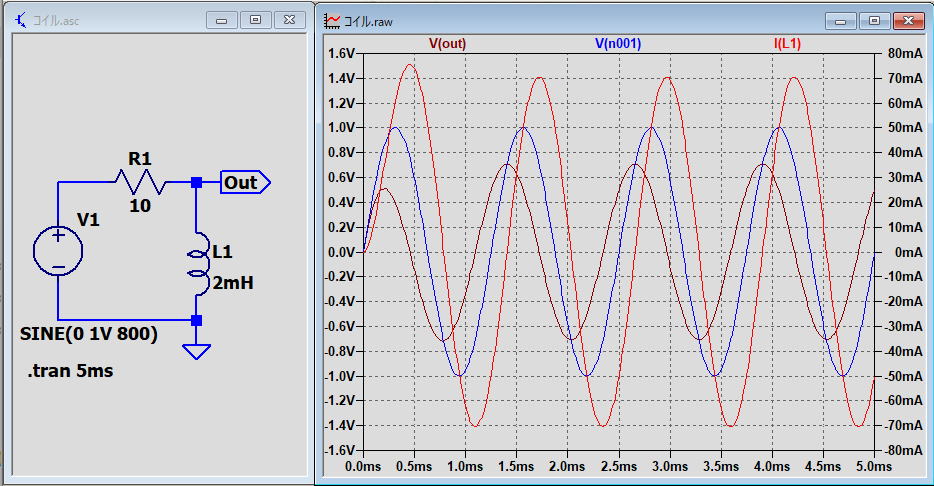
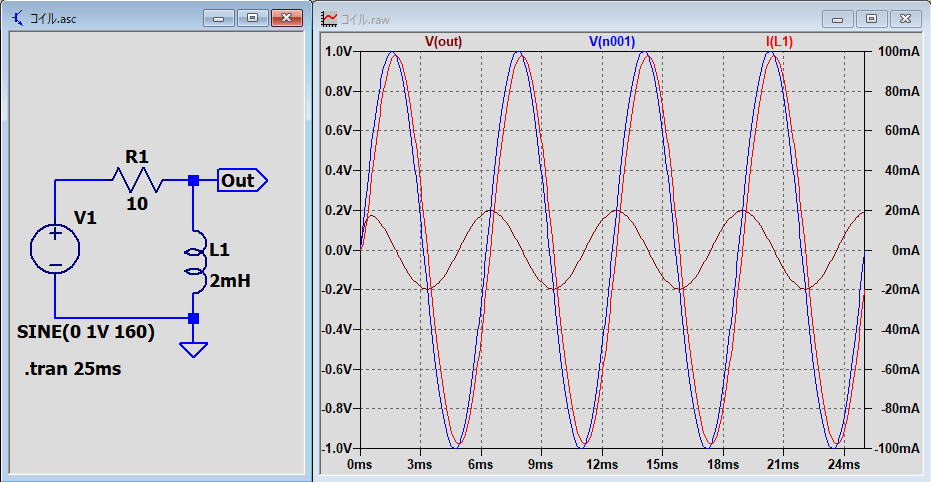
５．交流のRL回路（ハイパスフィルター） 交流電源に抵抗とコイルを組み合わせた回路の電圧と電流の変化について。 LTspiceで求めた波形を下記にしめします。 ■電源周波数10(kHz) V(n001)= 2 (Vp-p) V(out)　= 2(Vp-p) I(L1)　　=16(mAp-p) V(n001) = V1電圧 V(out) = Vout電圧 I(L1) = L1電流 ■電源周波数800(Hz) V(n001)= 2 (Vp-p) V(out)　= 1.4(Vp-p) I(L1)　　=140(mAp-p) V(n001) = V1電圧 V(out) = Vout電圧 I(L1) = L1電流 ■電源周波数160(Hz) V(n001)= 2 (Vp-p) V(out)　= 0.4(Vp-p) I(L1)　　=200(mAp-p) V(n001) = V1電圧 V(out) = Vout電圧 I(L1) = L1電流 なおハイパスフィルター関係には下記公式がある。 ゲイン　 　出力電圧 / 入力電圧　＝増幅率を言う　上記簡略式で言う　電源電圧 / コイル電圧 となる。 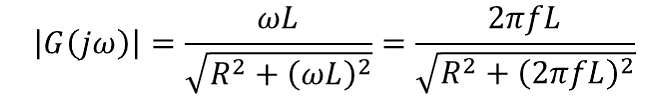　増幅率を電力dbで表示する場合は下記式になる。 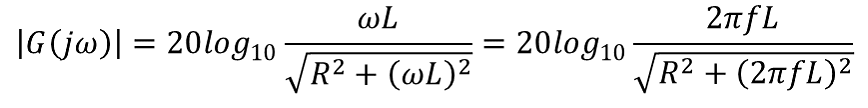位相差 　入力電圧と出力電圧の位相差を言います 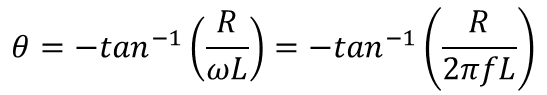カットオフ周波数 　電力値が半分になる周波数を言います。　db表記で-3dbです。 　従って電圧で表記する場合は1/√2 ≒ 0.7071 となる。 今回の緒元では10×103／(2×3.14×2) ≒　800(Hz)　 上記公式から作成出来るグラフを下記に示す。 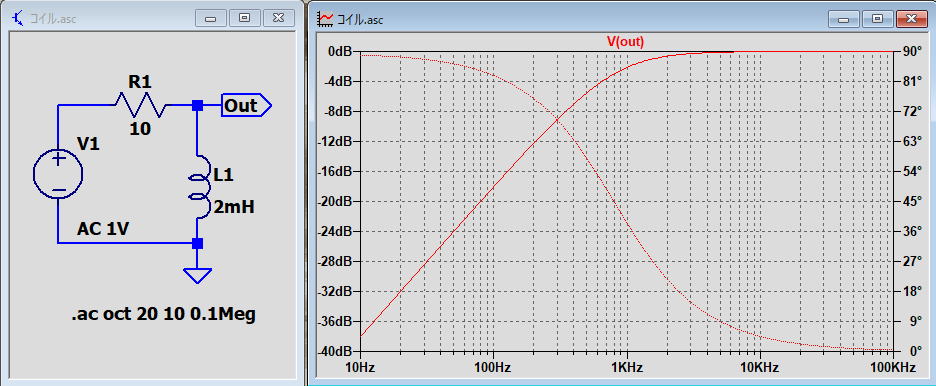実線がゲイン、点線(右下がり線)が位相です。 [目次に戻る]